Multi-parameter inference

Download notebook

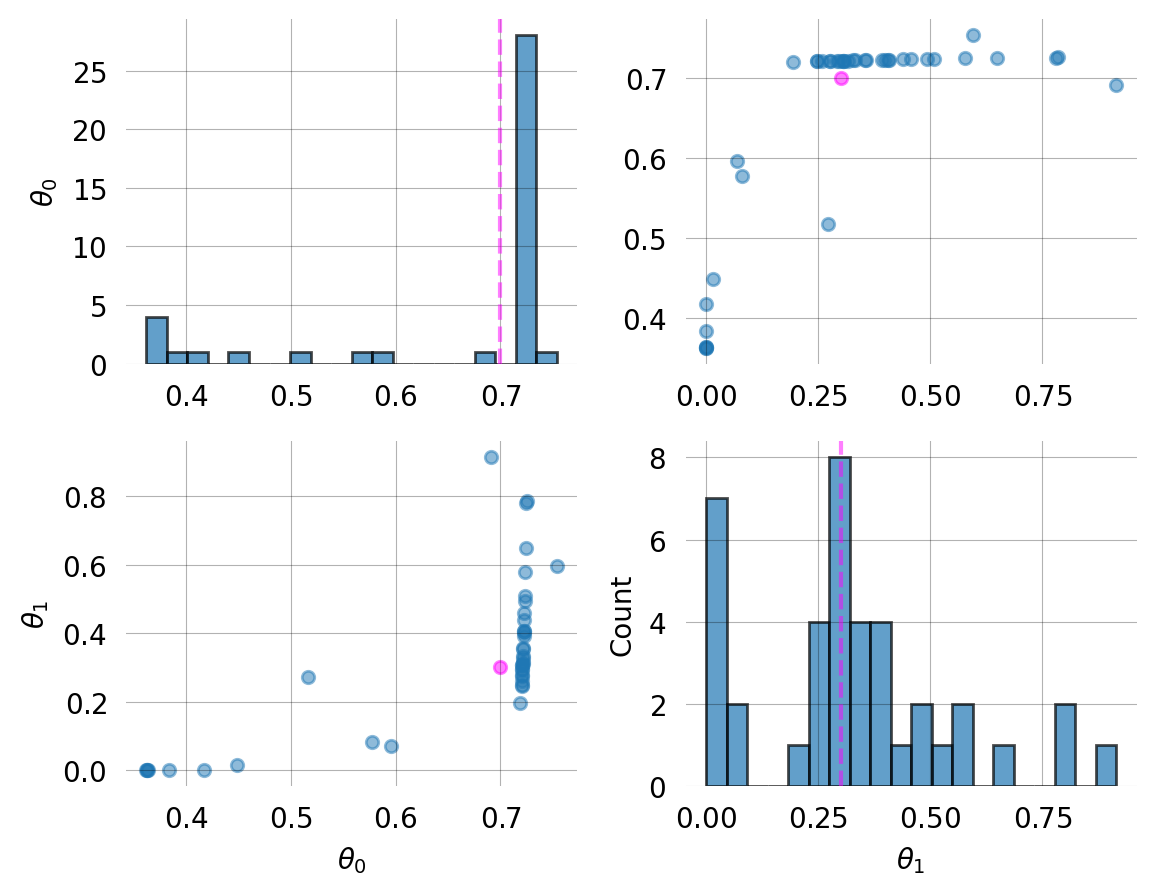
Lets try to estimate both coalescent and migration rate in a two population model.

from phasic import (
    Graph, with_ipv, set_log_level,
    StateIndexer, Property,
    GaussPrior, HalfCauchyPrior, ExpStepSize, ExpRegularization, 
    clear_caches, clear_jax_cache, clear_model_cache,
) # ALWAYS import phasic first to set jax backend correctly
import numpy as np
import jax.numpy as jnp
import pandas as pd
from typing import Optional
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
import seaborn as sns
from tqdm.auto import tqdm
from vscodenb import set_vscode_theme

np.random.seed(42)
set_vscode_theme()
sns.set_palette('tab10')

set_log_level('WARNING')

Overriding theme from NOTEBOOK_THEME environment variable. <phasic._DeviceListFilter object at 0x14f9bd6d0>

<phasic.logging_config.set_log_level at 0x17f354490>

nr_samples = 2

indexer = StateIndexer(
    descendants=[
    Property('pop1', min_value=0, max_value=nr_samples),
    Property('pop2', min_value=0, max_value=nr_samples),
    Property('in_pop', min_value=1, max_value=2),
])

initial = [0] * indexer.state_length

# set initial state with all lineages having one descendant at both loci
initial[indexer.descendants.props_to_index(pop1=1, pop2=0, in_pop=1)] = nr_samples

@with_ipv(initial)
def coalescent_islands(state):
    transitions = []

    if state[indexer.descendants.indices()].sum() <= 1:
        return transitions
    
    for i in range(indexer.descendants.state_length):
        if state[i] == 0: continue
        props_i = indexer.descendants.index_to_props(i)

        for j in range(i, indexer.descendants.state_length):
            if state[j] == 0: continue
            props_j = indexer.descendants.index_to_props(j)
            
            if props_j.in_pop != props_i.in_pop:
                continue

            same = int(i == j)
            if same and state[i] < 2:
                continue
            if not same and (state[i] < 1 or state[j] < 1):
                continue 

            child = state.copy()
            child[i] -= 1
            child[j] -= 1
            des_pop1 = props_i.pop1 + props_j.pop1
            des_pop2 = props_i.pop2 + props_j.pop2
            if des_pop1 <= nr_samples and des_pop2 <= nr_samples:
                k = indexer.descendants.props_to_index(
                    pop1=des_pop1, 
                    pop2=des_pop2, 
                    in_pop=props_i.in_pop
                    )
                child[k] += 1
                transitions.append([child, [state[i]*(state[j]-same)/(1+same), 0]])

        if state[i] > 0:
            child = state.copy()
            other_pop = 2 if props_i.in_pop == 1 else 1
            child = state.copy()
            child[i] -= 1
            k = indexer.descendants.props_to_index(
                pop1=props_i.pop1, 
                pop2=props_i.pop2, 
                in_pop=other_pop
                )
            child[k] += 1

            transitions.append([child, [0, state[i]]])

    return transitions

graph = Graph(coalescent_islands)   

true_theta = [0.7, 0.3]
graph.update_weights(true_theta)
graph.plot(rankdir='LR', by_index=lambda i: f"Desc in pop1: {indexer.index_to_props(i).descendants.pop1}")

Overriding theme from NOTEBOOK_THEME environment variable. <phasic._DeviceListFilter object at 0x14f9bd6d0>

graph.plot(rankdir='LR', by_state=lambda s: f"In pop1: {s[indexer.descendants.props_to_index(pop1=1)].sum()}")

Overriding theme from NOTEBOOK_THEME environment variable. <phasic._DeviceListFilter object at 0x14f9bd6d0>

observations = graph.sample(1000)

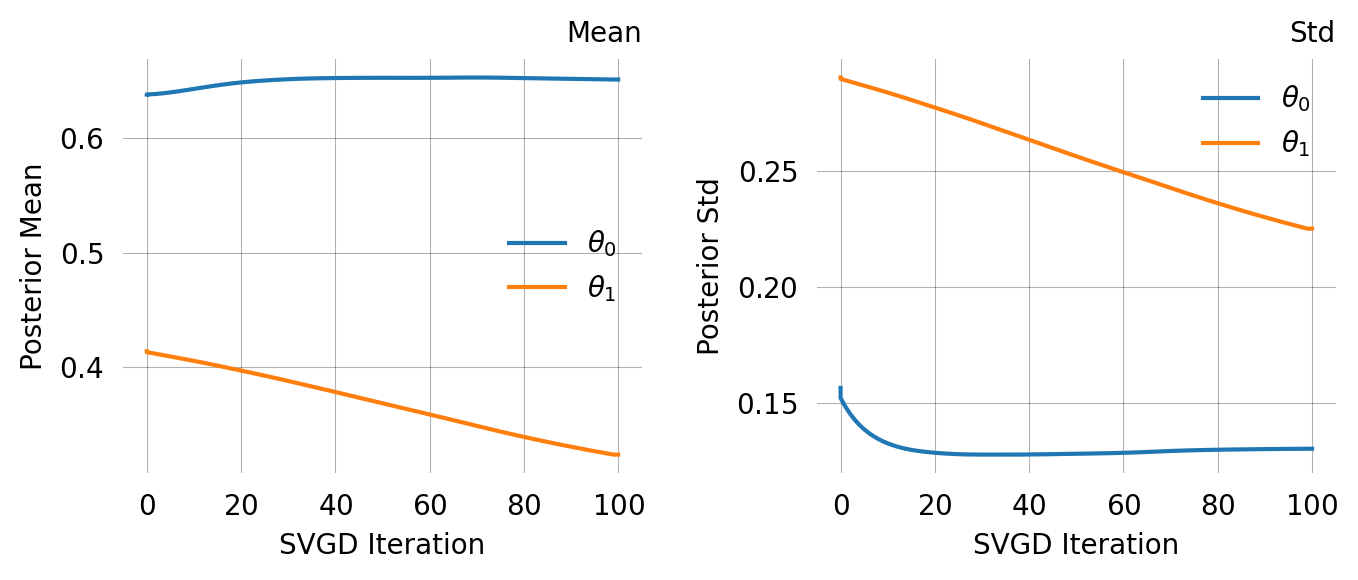
# quick run to get reasonable priors
svgd = graph.svgd(observations, n_particles=5, n_iterations=20)
res = svgd.get_results()
gauss_priors = []
for mean, std in zip(res['theta_mean'], res['theta_std']):
    gauss_priors.append(GaussPrior(mean, std))

# full run with informed priors
svgd = graph.svgd(observations, prior=gauss_priors)
svgd.summary()

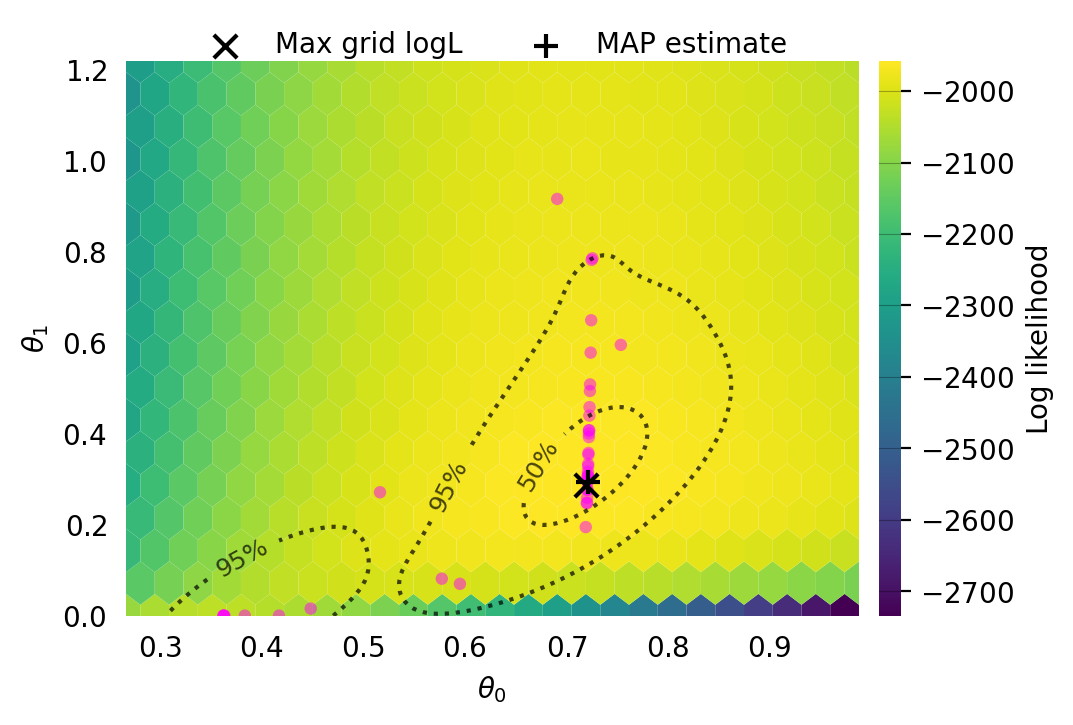
Parameter  Fixed      MAP        Mean       SD         HPD 95% lo   HPD 95% hi  
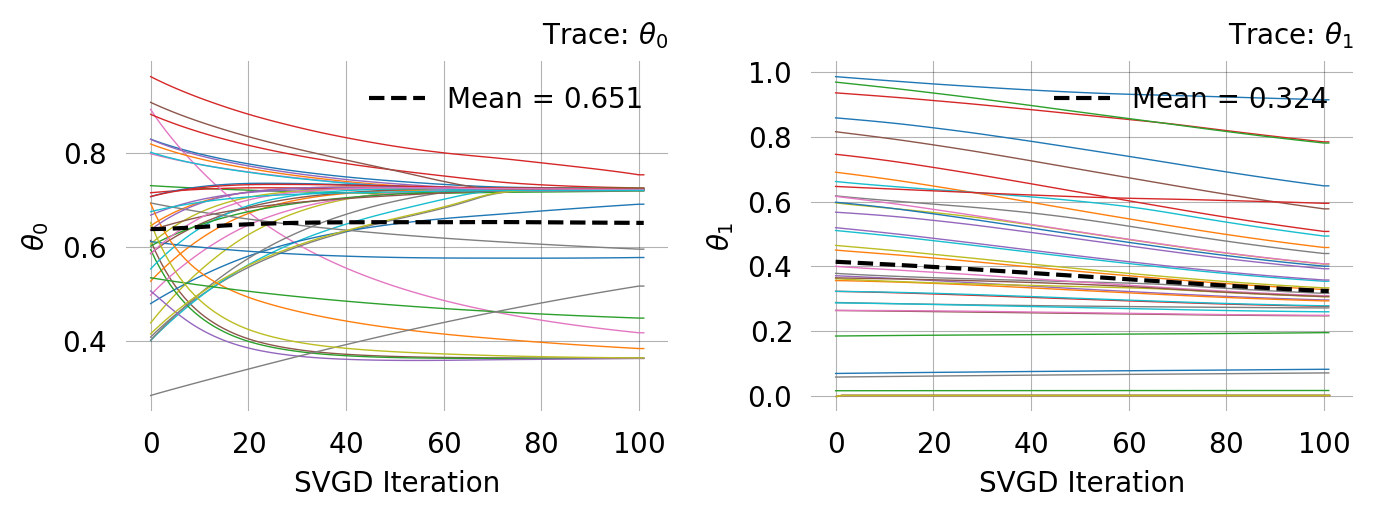
0          No         0.7210     0.6512     0.1303     0.3622       0.7249      
1          No         0.2929     0.3236     0.2250     0.0000       0.7813      

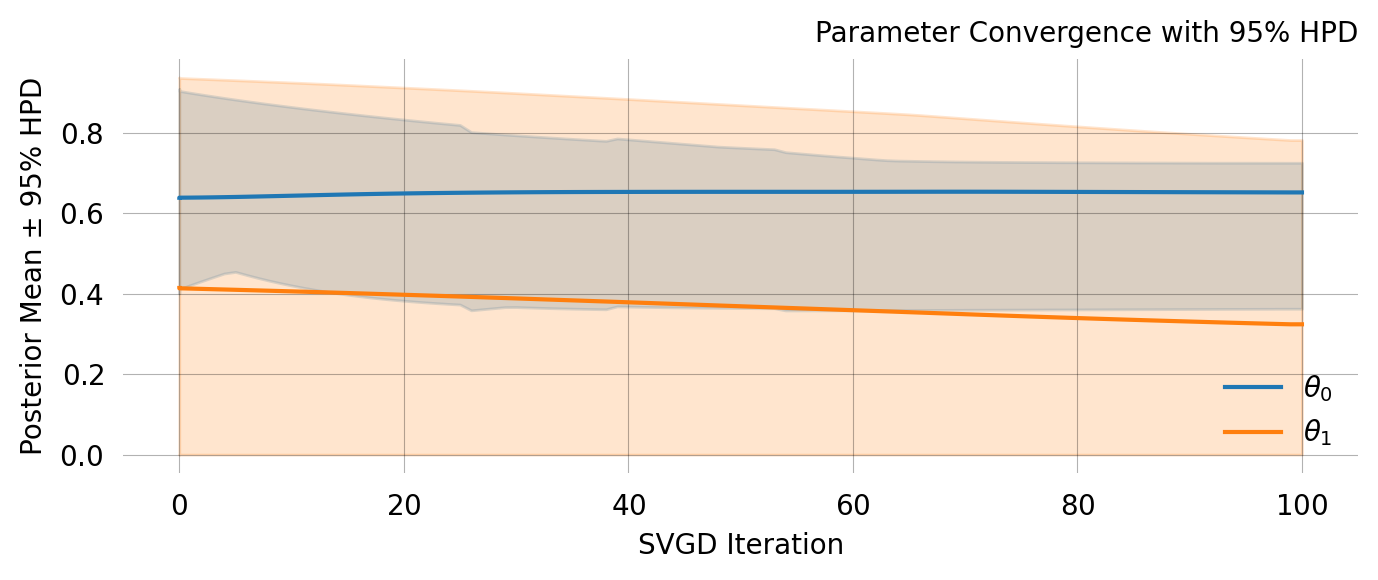
Particles: 40, Iterations: 100

svgd.plot_convergence()

<Figure size 640x480 with 0 Axes>

svgd.plot_ci()

svgd.plot_trace()

svgd.plot_hdr()

svgd.plot_pairwise(true_theta=true_theta)

#svgd.animate_pairwise(true_theta=true_theta)

Once Loop Reflect