Method of Moments

Data-informed priors via moment matching

A common challenge in Bayesian inference with SVGD is choosing sensible prior distributions. A vague prior may lead to slow convergence or poor exploration of the posterior, while an overly tight prior can bias the result. The method_of_moments method provides a principled way to construct data-informed priors by finding parameter estimates that match the model’s theoretical moments to the empirical moments of the observed data.

The method solves the nonlinear least-squares problem:

\hat{\theta}_{\text{MoM}} = \arg\min_{\theta > 0} \left\| \mathbf{m}(\theta) - \hat{\mathbf{m}} \right\|^2

where \mathbf{m}(\theta) are the model moments and \hat{\mathbf{m}} are the sample moments computed from the data. The standard error of the estimator is obtained via the delta method:

\text{Cov}(\hat\theta) \;=\; \left(\frac{\partial \mathbf{m}}{\partial \theta}\right)^{-1} \text{Cov}(\hat{\mathbf{m}}) \left(\frac{\partial \mathbf{m}}{\partial \theta}\right)^{-T}

where \text{Cov}(\hat{\mathbf{m}}) is estimated from the data. The point estimate and standard error are then used to construct Gaussian priors centred on the MoM estimate.

This is fast (seconds, not minutes) and gives SVGD a much better starting point than a generic prior.

from phasic import (
    Graph, with_ipv, GaussPrior, MoMResult, ProbMatchResult,
    Adam, ExpStepSize, clear_caches,
    StateIndexer, Property,
) # ALWAYS import phasic first to set jax backend correctly
import numpy as np
import jax.numpy as jnp
import matplotlib.pyplot as plt
import seaborn as sns

np.random.seed(42)
try:
    from vscodenb import set_vscode_theme
    set_vscode_theme()
except ImportError:
    pass
sns.set_palette('tab10')

Single-parameter model

We start with the simplest case: a single-parameter exponential model. The coalescent rate \theta governs how quickly lineages coalesce. For an exponential distribution, the method of moments has an analytical solution: \hat{\theta} = 1 / \bar{x}.

nr_samples = 4

@with_ipv([nr_samples]+[0]*(nr_samples-1))
def coalescent_1param(state):
    transitions = []
    for i in range(state.size):
        for j in range(i, state.size):            
            same = int(i == j)
            if same and state[i] < 2:
                continue
            if not same and (state[i] < 1 or state[j] < 1):
                continue 
            new = state.copy()
            new[i] -= 1
            new[j] -= 1
            new[i+j+1] += 1
            transitions.append([new, [state[i]*(state[j]-same)/(1+same)]])
    return transitions

graph = Graph(coalescent_1param)
graph.plot()

Sample observed data from the model with a known true parameter value:

true_theta = [7]
graph.update_weights(true_theta)
observed_data = graph.sample(1000)

Run method of moments to find the parameter estimate:

mom = graph.method_of_moments(observed_data)

MoM: theta_dim=1, n_free=1, nr_moments=4, n_features=1, n_equations=4
MoM: sample moments =
[0.21378016 0.07103006 0.03323121 0.01987239]
MoM: initial guess (full theta) = [6.95192796]
MoM: converged — `gtol` termination condition is satisfied.
MoM: theta = [6.95430573]
MoM: residual = 1.002189e-05
MoM: model moments =
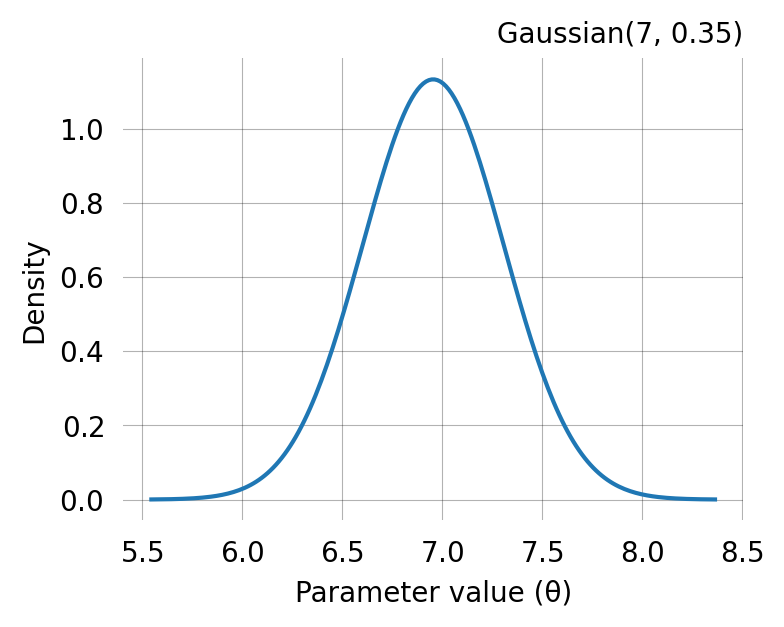
[0.21569371 0.07007285 0.03146742 0.01834498]

The result is a MoMResult dataclass containing the estimate, standard errors, and ready-to-use priors:

print(f"True theta:     {true_theta}")
print(f"MoM estimate:   {mom.theta}")
print(f"Std error:      {mom.std}")
print(f"Converged:      {mom.success}")
print(f"Residual:       {mom.residual:.2e}")

True theta:     [7]
MoM estimate:   [6.95430573]
Std error:      [0.17612875]
Converged:      True
Residual:       1.00e-05

The MoMResult also reports how well the model moments match the sample moments:

print(f"Sample moments: {mom.sample_moments}")
print(f"Model moments:  {mom.model_moments}")

Sample moments: [0.21378016 0.07103006 0.03323121 0.01987239]
Model moments:  [0.21569371 0.07007285 0.03146742 0.01834498]

Using MoM estimates as SVGD priors

The main purpose of method_of_moments is to produce informed priors for SVGD. The mom.prior attribute is a list of GaussPrior objects that can be passed directly to graph.svgd():

mom.prior[0].plot()

<Figure size 640x480 with 0 Axes>

svgd = graph.svgd(
    observed_data,
    prior=mom.prior,
    optimizer=Adam(0.25),
)
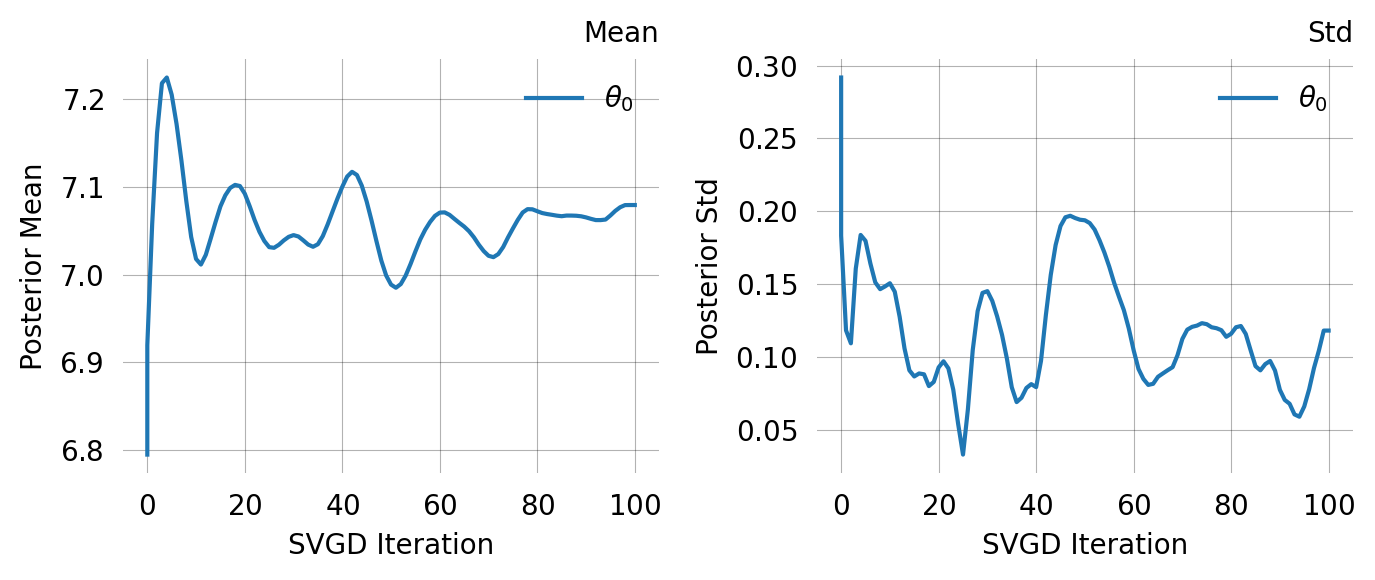
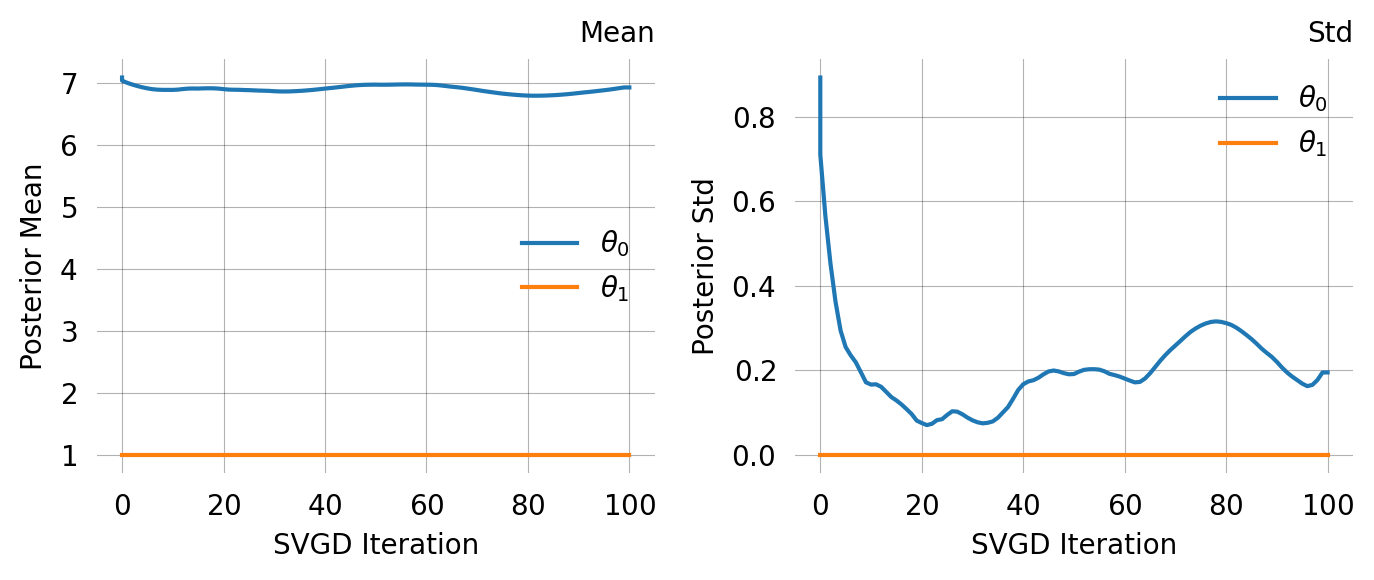
svgd.summary()
svgd.plot_convergence() ;

Parameter  Fixed      MAP        Mean       SD         HPD 95% lo   HPD 95% hi  
0          No         7.0606     7.0794     0.1180     6.7567       7.2409      

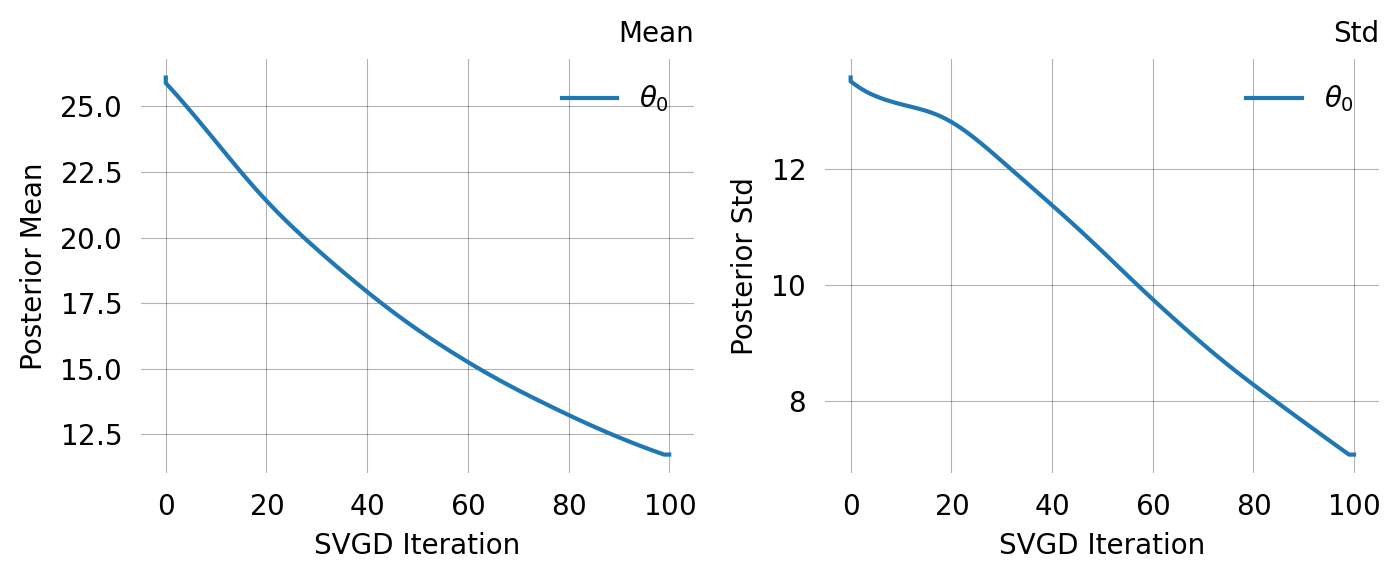
Particles: 24, Iterations: 100

Compare this to using a vague prior. The MoM-informed prior starts SVGD in the right region, leading to faster and more reliable convergence:

svgd_vague = graph.svgd(
    observed_data,
    prior=GaussPrior(ci=[0.1, 50]),  # very vague prior
    optimizer=Adam(0.25),
)
svgd_vague.summary()
svgd_vague.plot_convergence() ;

Parameter  Fixed      MAP        Mean       SD         HPD 95% lo   HPD 95% hi  
0          No         7.1091     11.7320    7.0768     6.4650       24.2832     

Particles: 24, Iterations: 100

Multi-parameter model

Method of moments is especially useful for multi-parameter models where choosing good priors by hand is difficult. Here we use a two-population island model with coalescent rate \theta_0 and migration rate \theta_1.

from phasic import StateIndexer, Property

nr_samples = 2

indexer = StateIndexer(
    descendants=[
    Property('pop1', min_value=0, max_value=nr_samples),
    Property('pop2', min_value=0, max_value=nr_samples),
    Property('in_pop', min_value=1, max_value=2),
])

initial = [0] * indexer.state_length
initial[indexer.descendants.props_to_index(pop1=1, pop2=0, in_pop=1)] = nr_samples

@with_ipv(initial)
def coalescent_islands(state):
    transitions = []
    if state[indexer.descendants.indices()].sum() <= 1:
        return transitions
    for i in range(indexer.descendants.state_length):
        if state[i] == 0: continue
        props_i = indexer.descendants.index_to_props(i)
        for j in range(i, indexer.descendants.state_length):
            if state[j] == 0: continue
            props_j = indexer.descendants.index_to_props(j)
            if props_j.in_pop != props_i.in_pop:
                continue
            same = int(i == j)
            if same and state[i] < 2:
                continue
            if not same and (state[i] < 1 or state[j] < 1):
                continue 
            child = state.copy()
            child[i] -= 1
            child[j] -= 1
            des_pop1 = props_i.pop1 + props_j.pop1
            des_pop2 = props_i.pop2 + props_j.pop2
            if des_pop1 <= nr_samples and des_pop2 <= nr_samples:
                k = indexer.descendants.props_to_index(
                    pop1=des_pop1, pop2=des_pop2, in_pop=props_i.in_pop)
                child[k] += 1
                transitions.append([child, [state[i]*(state[j]-same)/(1+same), 0]])
        if state[i] > 0:
            child = state.copy()
            other_pop = 2 if props_i.in_pop == 1 else 1
            child[i] -= 1
            k = indexer.descendants.props_to_index(
                pop1=props_i.pop1, pop2=props_i.pop2, in_pop=other_pop)
            child[k] += 1
            transitions.append([child, [0, state[i]]])
    return transitions

graph = Graph(coalescent_islands)
graph.plot()

true_theta = [0.7, 0.3]
graph.update_weights(true_theta)
observed_data = graph.sample(1000)

Run method of moments on the two-parameter model:

mom = graph.method_of_moments(observed_data)

MoM: theta_dim=2, n_free=2, nr_moments=4, n_features=1, n_equations=4
MoM: sample moments =
[2.89041844e+00 2.19034775e+01 2.64810856e+02 4.27038260e+03]
MoM: initial guess (full theta) = [ 0.66306831 12.49249157]
MoM: converged — Both `ftol` and `xtol` termination conditions are satisfied.
MoM: theta = [0.68703279 0.28364415]
MoM: residual = 3.242595e-02
MoM: model moments =
[2.91106921e+00 2.20801995e+01 2.64783140e+02 4.27038342e+03]

print(f"True theta:     {true_theta}")
print(f"MoM estimate:   {mom.theta}")
print(f"Std error:      {mom.std}")
print(f"Converged:      {mom.success}")

True theta:     [0.7, 0.3]
MoM estimate:   [0.68703279 0.28364415]
Std error:      [0.04358689 0.08585278]
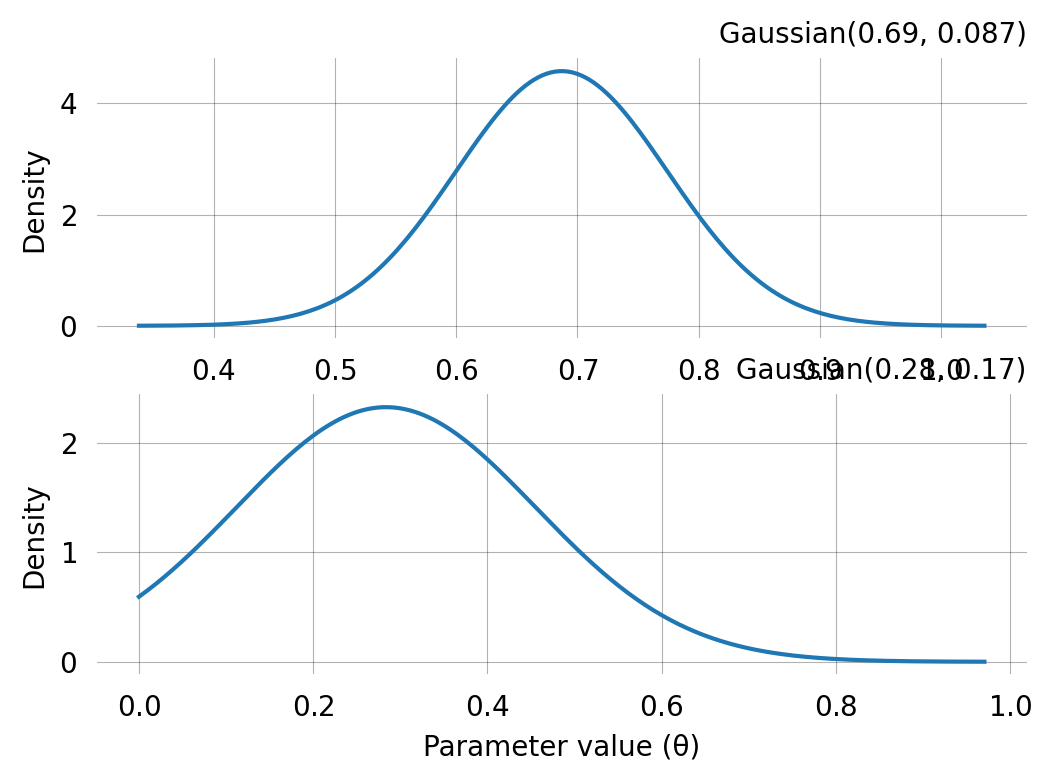
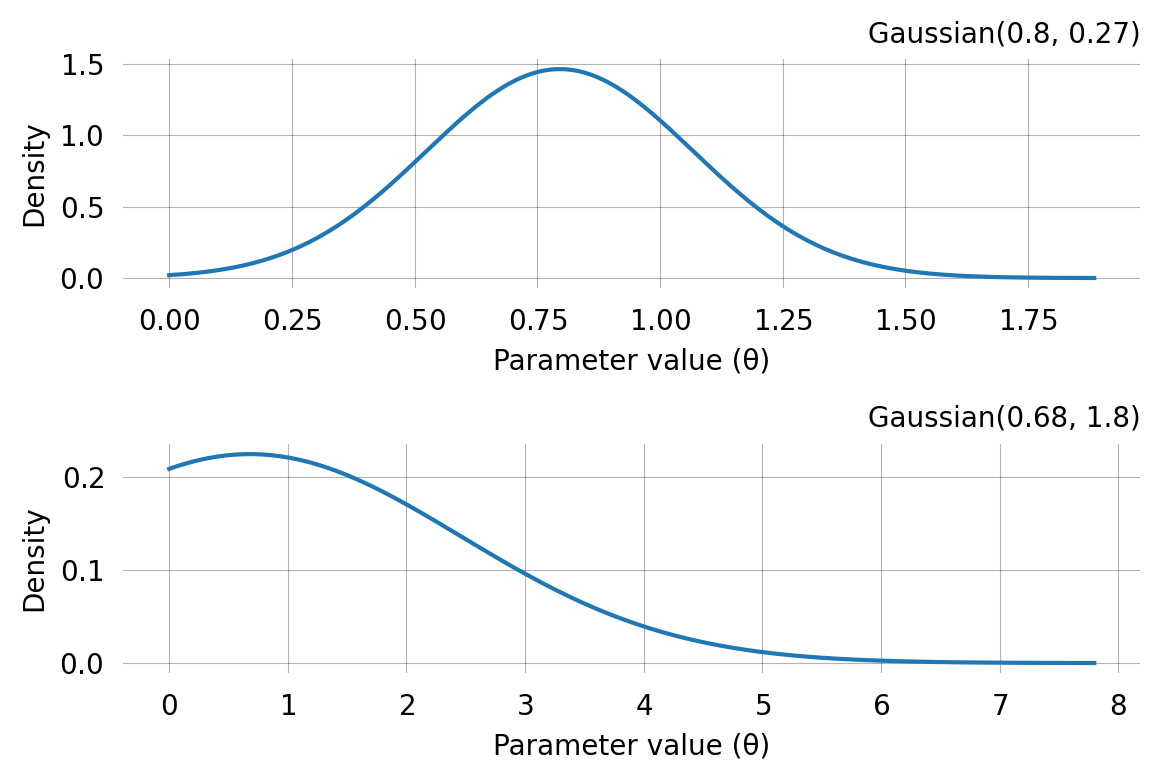
Converged:      True

len(mom.prior)

fig, axes = plt.subplots(len(mom.prior), 1, figsize=(6,4))
print(axes)
for i, prior in enumerate(mom.prior):
    prior.plot(return_ax=True, ax=axes[i])

[<Axes: > <Axes: >]

Use the MoM priors for SVGD inference:

svgd = graph.svgd(
    observed_data,
    prior=mom.prior,
    optimizer=Adam(0.25),
)
svgd.summary()
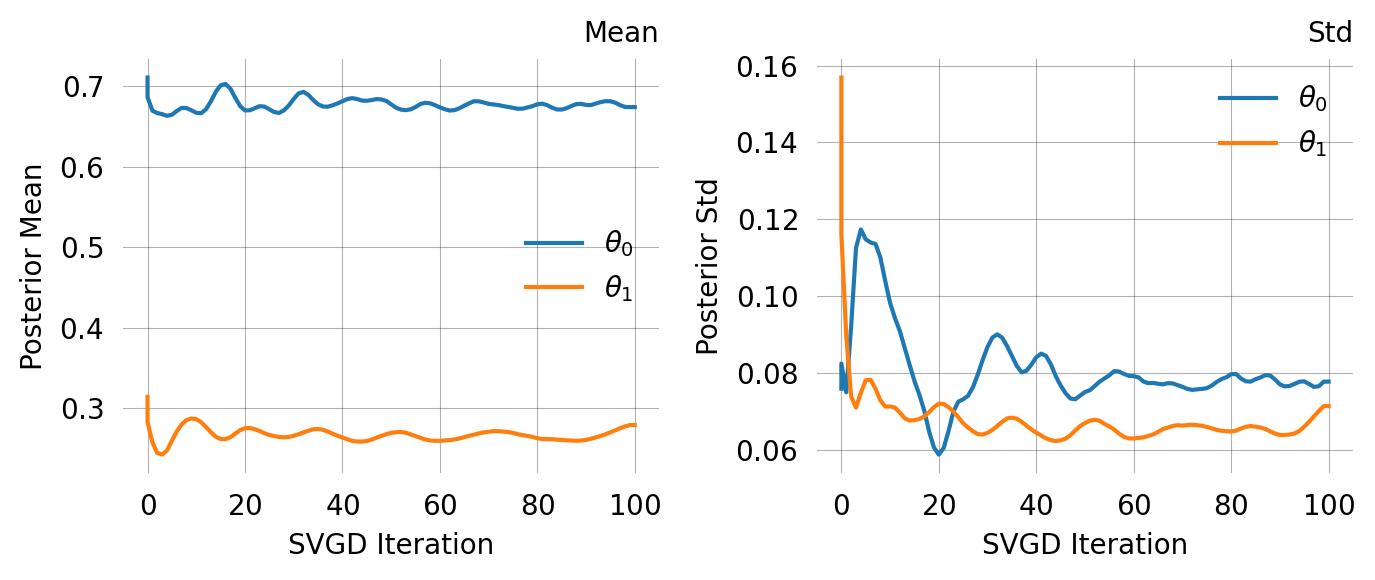
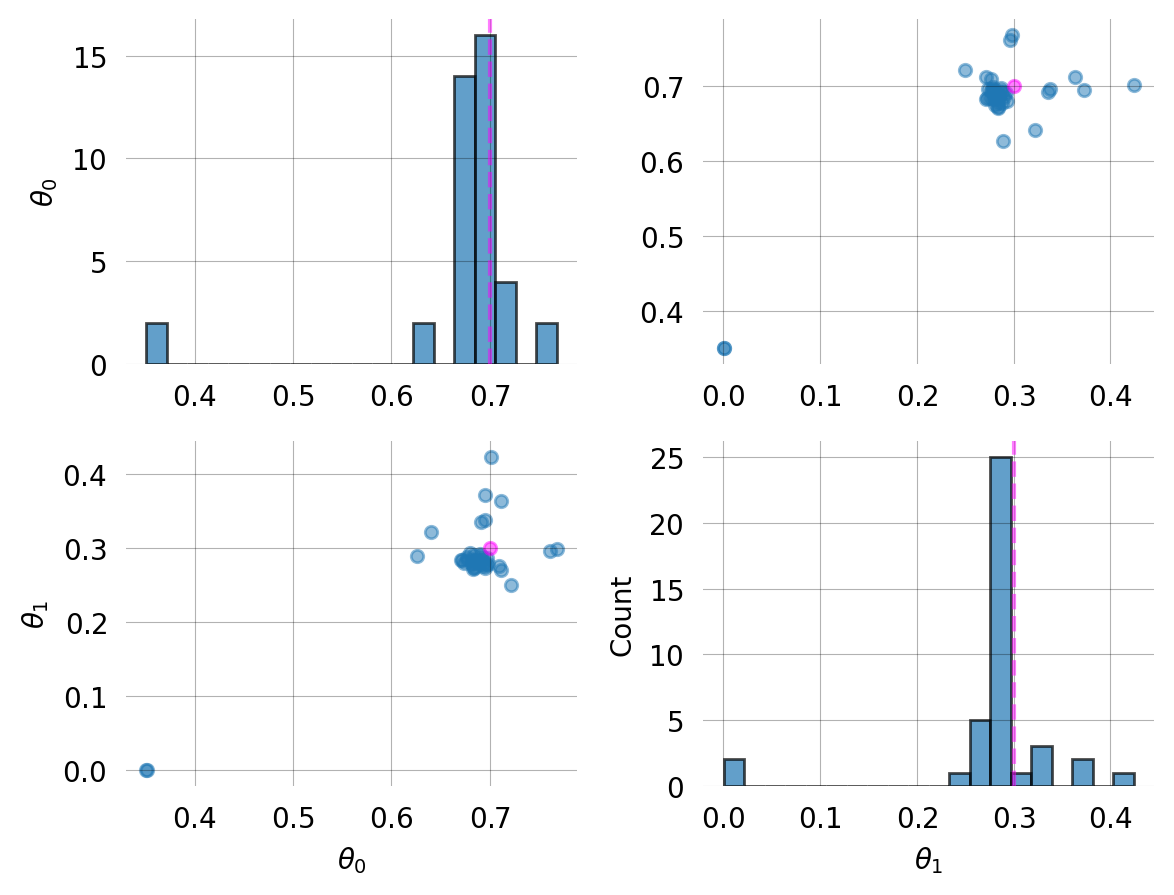
svgd.plot_convergence() ;

Parameter  Fixed      MAP        Mean       SD         HPD 95% lo   HPD 95% hi  
0          No         0.6944     0.6742     0.0777     0.6259       0.7680      
1          No         0.2802     0.2794     0.0714     0.2500       0.4239      

Particles: 40, Iterations: 100

svgd.plot_pairwise(true_theta=true_theta)

Fixed parameters

When some parameters are known, you can fix them during moment matching. The fixed argument takes a list of (index, value) tuples. Only the free parameters are optimised, and the returned prior list contains None at the fixed positions.

Here we fix the coalescent rate and estimate only the migration rate:

mom_fixed = graph.method_of_moments(
    observed_data,
    fixed=[(0, 0.7)],  # fix theta[0] (coalescent rate) at 0.7
)

print(f"MoM estimate:  {mom_fixed.theta}")
print(f"Priors:        {mom_fixed.prior}")
print(f"  theta[0] prior is None (fixed): {mom_fixed.prior[0] is None}")
print(f"  theta[1] prior:                 mean={mom_fixed.prior[1].mu:.3f}, std={mom_fixed.prior[1].sigma:.3f}")

MoM: theta_dim=2, n_free=1, nr_moments=4, n_features=1, n_equations=4
MoM: sample moments =
[2.89041844e+00 2.19034775e+01 2.64810856e+02 4.27038260e+03]
MoM: initial guess (full theta) = [0.7        8.21283765]
MoM: converged — Both `ftol` and `xtol` termination conditions are satisfied.
MoM: theta = [0.7        0.26600949]
MoM: residual = 6.416370e+00
MoM: model moments =
[2.85714286e+00 2.16969082e+01 2.62288310e+02 4.27047933e+03]
MoM estimate:  [0.7        0.26600949]
Priors:        [None, <phasic.svgd.GaussPrior object at 0x360b132d0>]
  theta[0] prior is None (fixed): True
  theta[1] prior:                 mean=0.266, std=0.132

The fixed parameter priors integrate seamlessly with SVGD’s fixed argument:

svgd_fixed = graph.svgd(
    observed_data,
    prior=mom_fixed.prior,
    fixed=[(0, 0.7)],
    optimizer=Adam(0.25),
)
svgd_fixed.summary()

Parameter  Fixed      MAP        Mean       SD         HPD 95% lo   HPD 95% hi  
0          Yes        0.7000     NA         NA         NA           NA          
1          No         0.2803     0.2828     0.0310     0.2392       0.3174      

Particles: 40, Iterations: 100

Multi-feature observations with rewards

For models where observations are reward-transformed (e.g. branch lengths contributing to different mutation categories in population genetics), method of moments can match moments per feature. Each feature has its own reward vector, and the combined system of equations constrains the parameters.

graph_1p = Graph(coalescent_1param)
true_theta_1p = [7]
graph_1p.update_weights(true_theta_1p)

# Create reward vectors — each row is a feature's reward across all vertices
states = graph_1p.states().T
rewards = states[:-1]  # one row per feature (e.g. singleton, doubleton, tripleton branch lengths)
print(f"Reward matrix shape: {rewards.shape}  (n_features={rewards.shape[0]}, n_vertices={rewards.shape[1]})")
print(f"Rewards:\n{rewards}")

Reward matrix shape: (3, 6)  (n_features=3, n_vertices=6)
Rewards:
[[0 4 2 0 1 0]
 [0 0 1 2 0 0]
 [0 0 0 0 1 0]]

# Sample multi-feature observations (each SNP contributes to one feature)
n_obs = 10000
n_features = rewards.shape[0]
observed_data_2d = np.zeros((n_obs * n_features, n_features), dtype=float)
observed_data_2d[:] = np.nan
for i in range(n_features):
    observed_data_2d[(i*n_obs):((i+1)*n_obs), i] = graph_1p.sample(n_obs, rewards=rewards[i])
np.random.shuffle(observed_data_2d)

print(f"Observation shape: {observed_data_2d.shape}")
print(f"First 5 rows (NaN = unobserved feature):")
print(observed_data_2d[:5])

Observation shape: (30000, 3)
First 5 rows (NaN = unobserved feature):
[[0.12124815        nan        nan]
 [0.36418885        nan        nan]
 [       nan        nan 0.10161367]
 [0.03089352        nan        nan]
 [0.60967296        nan        nan]]

mom_multi = graph_1p.method_of_moments(
    observed_data_2d,
    rewards=rewards,
)

print(f"True theta:     {true_theta_1p}")
print(f"MoM estimate:   {mom_multi.theta}")
print(f"Converged:      {mom_multi.success}")
print(f"\nSample moments (n_features x nr_moments):\n{mom_multi.sample_moments}")
print(f"\nModel moments (n_features x nr_moments):\n{mom_multi.model_moments}")

MoM: theta_dim=1, n_free=1, nr_moments=4, n_features=3, n_equations=12
MoM: sample moments =
[[0.28569414 0.11867841 0.06469594 0.04371687]
 [0.1425845  0.06761152 0.05566143 0.06176143]
 [0.09469394 0.02795647 0.01293379 0.00821446]]
MoM: initial guess (full theta) = [6.95192796]
MoM: converged — `gtol` termination condition is satisfied.
MoM: theta = [7.00133145]
MoM: residual = 1.515105e-05
MoM: model moments =
[[0.28565995 0.11786899 0.06345585 0.04217254]
 [0.14282998 0.06800134 0.05633325 0.06399868]
 [0.09521998 0.02720054 0.01165516 0.00665882]]
True theta:     [7]
MoM estimate:   [7.00133145]
Converged:      True

Sample moments (n_features x nr_moments):
[[0.28569414 0.11867841 0.06469594 0.04371687]
 [0.1425845  0.06761152 0.05566143 0.06176143]
 [0.09469394 0.02795647 0.01293379 0.00821446]]

Model moments (n_features x nr_moments):
[[0.28565995 0.11786899 0.06345585 0.04217254]
 [0.14282998 0.06800134 0.05633325 0.06399868]
 [0.09521998 0.02720054 0.01165516 0.00665882]]

The multivariate MoM priors can be used with multivariate SVGD:

FIXME:

svgd_multi = graph_1p.svgd( observed_data_2d, rewards=rewards, prior=mom_multi.prior, optimizer=Adam(0.25), ) svgd_multi.summary() svgd_multi.plot_convergence() ;

Controlling the number of moments

By default, method_of_moments automatically selects the number of moments to create an overdetermined system: max(2 × n_free_params, 4) moments per feature. This typically gives robust estimates without any tuning.

You can override the automatic selection by passing nr_moments explicitly. If you specify fewer moment equations than free parameters, the method automatically increases nr_moments:

FIXME:

graph_2p = Graph(coalescent_islands) graph_2p.update_weights([0.7, 0.3]) data_2p = graph_2p.sample(1000)

Ask for 1 moment with 2 free params -> auto-increases

mom_auto = graph_2p.method_of_moments(data_2p, nr_moments=1)

Using more moments than parameters (overdetermined system) can improve robustness:

mom_over = graph_2p.method_of_moments(data_2p, nr_moments=4) print(f”nr_moments=4, theta = {mom_over.theta}“) print(f”Residual: {mom_over.residual:.2e}“)

Adjusting the prior width

The std_multiplier parameter controls how wide the MoM-derived prior is relative to the asymptotic standard error. A larger multiplier gives a wider, more permissive prior:

# Default: std_multiplier=2.0
mom_default = graph.method_of_moments(observed_data, verbose=False)
print(f"std_multiplier=2.0 -> prior std = {mom_default.prior[0].sigma:.4f}")

# Wider prior
mom_wide = graph.method_of_moments(observed_data, std_multiplier=5.0, verbose=False)
print(f"std_multiplier=5.0 -> prior std = {mom_wide.prior[0].sigma:.4f}")

# Tighter prior
mom_tight = graph.method_of_moments(observed_data, std_multiplier=1.0, verbose=False)
print(f"std_multiplier=1.0 -> prior std = {mom_tight.prior[0].sigma:.4f}")

std_multiplier=2.0 -> prior std = 0.0872
std_multiplier=5.0 -> prior std = 0.2179
std_multiplier=1.0 -> prior std = 0.0436

Choosing std_multiplier

2.0 (default): A good balance — wide enough to let the data speak, tight enough to aid convergence.
1.0: Tight prior. Use when you trust the MoM estimate and want fast convergence.
3.0–5.0: Wide prior. Use when you want SVGD to explore broadly, using MoM only as a rough guide.

The MoMResult object

The method_of_moments method returns a MoMResult dataclass with the following fields:

Field	Type	Description
`theta`	`np.ndarray`	MoM parameter estimate
`std`	`np.ndarray`	Standard error of the MoM estimator (delta method)
`prior`	`list`	List of `GaussPrior` objects (or `None` for fixed params)
`success`	`bool`	Whether the optimisation converged
`residual`	`float`	Sum of squared residuals
`sample_moments`	`np.ndarray`	Empirical moments from the data
`model_moments`	`np.ndarray`	Model moments at the solution
`message`	`str`	Solver status message

The standard errors quantify the sampling uncertainty of the MoM estimator — how much theta would change with a different random sample of the same size. They are computed via the delta method, propagating the covariance of the sample moments through the moment-matching equations. These errors scale as 1/\sqrt{n} with the sample size n.

Complete workflow

Putting it all together, the recommended workflow for inference is:

Build the parameterized graph
MoM — get data-informed priors in seconds
SVGD — run full Bayesian inference with the MoM priors
Diagnose — check convergence and posterior

# 1. Build model
graph = Graph(coalescent_islands)

# 2. Method of moments
true_theta = [0.7, 0.3]
graph.update_weights(true_theta)
observations = graph.sample(100)

mom = graph.method_of_moments(observations)

MoM: theta_dim=2, n_free=2, nr_moments=4, n_features=1, n_equations=4
MoM: sample moments =
[   2.42023367   14.23982075  127.14644098 1490.61257429]
MoM: initial guess (full theta) = [0.910071   7.07235481]
MoM: converged — Both `ftol` and `xtol` termination conditions are satisfied.
MoM: theta = [0.79598546 0.6802256 ]
MoM: residual = 6.607437e-02
MoM: model moments =
[   2.51260871   14.47329878  127.09145244 1490.61491816]

fig, axes = plt.subplots(len(mom.prior), 1, figsize=(6,4))
for i, prior in enumerate(mom.prior):
    prior.plot(return_ax=True, ax=axes[i])
plt.tight_layout()

# from phasic import configure
# configure(
#     force_high_precision=True,
#     mpfr_precision_bits=256
# )

# svgd = graph.svgd(
#     observations,
#     prior=mom.prior,
#     learning_rate=ExpStepSize(first_step=0.01, last_step=0.001, tau=20.0),
#     n_iterations=100,
# )

# svgd.summary()

# svgd.plot_convergence()

# svgd.plot_trace()

# svgd.plot_pairwise(true_theta=true_theta)

# svgd.plot_hdr()

Joint probability models

For joint probability graphs — created via graph.joint_prob_graph() — observations are feature-count tuples (e.g., [0, 1, 0, 0]) rather than continuous times. The model outputs a probability table, not a PDF/PMF with moments, so standard moment matching does not apply.

The probability_matching() method handles this case by matching the empirical probability distribution to the model probability distribution:

\hat{\theta}_{\text{PM}} = \arg\min_{\theta > 0} \left\| \mathbf{p}_{\text{model}}(\theta) - \hat{\mathbf{p}} \right\|^2

where \hat{\mathbf{p}} are the empirical proportions of each observation pattern. Standard errors are obtained via the delta method with the multinomial covariance:

\text{Cov}(\hat{p}_i, \hat{p}_j) = \frac{\delta_{ij} p_i - p_i p_j}{n}

from functools import partial
from itertools import combinations_with_replacement

all_pairs = partial(combinations_with_replacement, r=2)

# Build the coalescent base graph
nr_samples = 3

indexer = StateIndexer(
    lineage=[
        Property('descendants', min_value=1, max_value=nr_samples),
    ]
)

@with_ipv([nr_samples]+[0]*(nr_samples-1))
def coalescent_1param(state):
    transitions = []
    for i, j in all_pairs(indexer.lineage):
        p1 = indexer.lineage.index_to_props(i)
        p2 = indexer.lineage.index_to_props(j)
        same = int(i == j)
        if same and state[i] < 2:
            continue
        if not same and (state[i] < 1 or state[j] < 1):
            continue
        new = state.copy()
        new[i] -= 1
        new[j] -= 1
        descendants = p1.descendants + p2.descendants
        k = indexer.lineage.props_to_index(descendants=descendants)
        new[k] += 1
        transitions.append([new, [state[i]*(state[j]-same)/(1+same)]])
    return transitions

base_graph = Graph(coalescent_1param)

# Create joint probability graph
mutation_rate = 1.0
joint_graph = base_graph.joint_prob_graph(
    indexer, tot_reward_limit=2, mutation_rate=mutation_rate
)
joint_graph.joint_prob_table()

	descendants_1	descendants_2	descendants_3	prob
t_vertex_index
4	0	0	0	0.166667
8	1	0	0	0.138889
11	0	1	0	0.055556
13	2	0	0	0.043981
14	1	1	0	0.032407
15	0	2	0	0.009259

Sample observations from the joint probability table:

true_theta = [7.0, mutation_rate]
joint_graph.update_weights(true_theta)

# Sample from the joint probability table
table = joint_graph.joint_prob_table()
p = table['prob'].to_numpy()
p = p / p.sum()
feature_cols = table.columns[:-1]

np.random.seed(42)
n_obs = 2000
sampled_rows = np.random.choice(len(table), size=n_obs, p=p)
observations = [tuple(int(x) for x in row) for row in table.iloc[sampled_rows][feature_cols].values]
print(f"Sampled {n_obs} observations, first 5: {observations[:5]}")

Sampled 2000 observations, first 5: [(0, 0, 0), (2, 0, 0), (1, 0, 0), (0, 0, 0), (0, 0, 0)]

Run probability_matching() with the mutation rate fixed:

pm = joint_graph.probability_matching(
    observations,
    fixed=[(1, mutation_rate)],
)

print(f"True theta:     {true_theta}")
print(f"PM estimate:    {pm.theta}")
print(f"Std error:      {pm.std}")
print(f"Converged:      {pm.success}")
print(f"Residual:       {pm.residual:.2e}")

ProbMatch: theta_dim=2, n_free=1, n_obs=2000, n_unique_obs=6
ProbMatch: initial guess (full theta) = [7.88046282 1.        ]
ProbMatch: converged — `gtol` termination condition is satisfied.
ProbMatch: theta = [7.00204262 1.        ]
ProbMatch: residual = 3.839769e-05
True theta:     [7.0, 1.0]
PM estimate:    [7.00204262 1.        ]
Std error:      [0.35605011 0.        ]
Converged:      True
Residual:       3.84e-05

The ProbMatchResult includes the empirical and model probabilities at the solution:

import pandas as pd
pd.DataFrame({
    'vertex_index': pm.unique_indices,
    'empirical_prob': pm.empirical_probs,
    'model_prob': pm.model_probs,
})

	vertex_index	empirical_prob	model_prob
0	4	0.6935	0.694502
1	8	0.1590	0.163940
2	11	0.0785	0.077149
3	13	0.0310	0.029057
4	14	0.0295	0.026782
5	15	0.0085	0.008570

The .prior list can be passed directly to graph.svgd(), just like MoMResult.prior:

svgd_jp = joint_graph.svgd(
    observations,
    prior=pm.prior,
    fixed=[(1, mutation_rate)],
    optimizer=Adam(0.25),
)

svgd_jp.summary()

Parameter  Fixed      MAP        Mean       SD         HPD 95% lo   HPD 95% hi  
0          No         6.8955     6.9337     0.1944     6.5354       7.2389      
1          Yes        1.0000     NA         NA         NA           NA          

Particles: 40, Iterations: 100

svgd_jp.plot_convergence()

One-step alternative: `DataPrior`

The two-step pattern of running method_of_moments (or probability_matching) followed by passing .prior to graph.svgd() is common enough that DataPrior wraps it into a single object. It auto-detects whether the graph is a joint probability graph and calls the appropriate estimation method.

# Before (two steps):
mom = graph.method_of_moments(data, fixed=[(1, 1.0)])
svgd = graph.svgd(data, prior=mom.prior, fixed=[(1, 1.0)])

# After (one step):
svgd = graph.svgd(data, prior=DataPrior(graph, data, fixed=[(1, 1.0)]), fixed=[(1, 1.0)])

# from phasic import DataPrior

# # Standard graph — DataPrior calls method_of_moments internally
# graph_dp = Graph(coalescent_islands)
# graph_dp.update_weights([0.7, 0.3])
# data_dp = graph_dp.sample(500)

# dp = DataPrior(graph_dp, data_dp, sd=2.0)
# print(dp)
# print(f"Underlying method: {dp.method}")
# print(f"Theta estimate:    {dp.theta}")
# print(f"Converged:         {dp.success}")

# # Use directly as the prior argument
# svgd_dp = graph_dp.svgd(data_dp, prior=dp, n_iterations=50, verbose=False)
# svgd_dp.summary()

# # Joint probability graph — DataPrior calls probability_matching internally
# dp_joint = DataPrior(
#     joint_graph, observations,
#     fixed=[(1, mutation_rate)],
# )
# print(dp_joint)
# print(f"Underlying method: {dp_joint.method}")

Data-informed priors via moment matching

Single-parameter model

Using MoM estimates as SVGD priors

Multi-parameter model

Fixed parameters

Multi-feature observations with rewards

FIXME:

Controlling the number of moments

FIXME:

Ask for 1 moment with 2 free params -> auto-increases

Adjusting the prior width

The MoMResult object

Complete workflow

Joint probability models

One-step alternative: DataPrior

One-step alternative: `DataPrior`